Page de Titre Table détaillée

Cours d'infographie    Chapitre 2 :Engineering Assisté par Ordinateur

I.S.I. Gramme   - Liège

Optimisation  Eléments finis  Analyse d'une structure  Simulation  Interface avec l'ingénieur

L'EAO recouvre toutes les techniques informatiques d'aide à l'ingénieur. On y retrouve principalement des logiciels de calcul. Tous les domaines ont leurs logiciels spécifiques : thermique, mécanique, optique, chimie, résistance des matériaux, mécanique des fluides. Sauf dans les cas simples (poutre sur deux appuis, par exemple), les formules de calculs simples ne sont pas applicables. Il faut alors réduire le problème à une série de sous-problèmes plus simples.

On remplace donc une structure complexe par un grand nombre de structure simples répondant à des lois simples. L'interaction entre ces divers éléments doit répondre à des critères de continuité entre éléments : c'est la méthode des éléments finis. Elle permet la vérification a posteriori d'une solution donnée.

On peut aussi laisser libres certaines données et demander au logiciel de leur trouver une valeur optimale. Par exemple, on donne la vue en plan d'une poutre et son chargement, et le programme donnera l'épaisseur de la poutre en chacun de ses points (en vérification simple, on aurait donné l'épaisseur et le calcul aurait rendu la contrainte dans le matériau).

La méthode des éléments finis est une méthode d'analyse des structures par laquelle on recherche la répartition ou champ des contraintes qui règnent dans la structure étudiée. Le champ des contraintes calculées doit être l'image d'un système de forces intérieures et extérieures se trouvant partout en équilibre. Simultanément, les déplacements doivent rester continus: ce sont les conditions d'équilibre et de compatibilité.

Dans un premier temps, il s'agit de définir les équations régissant la solution et qui satisfont aux conditions d'équilibre et de compatibilité. Il n'est pas toujours aisé de trouver les équations qui représentent le plus fidèlement possible les conditions réelles, c'est-à-dire toutes les complexités intervenant dans la géométrie, le chargement, et les propriétés intrinsèques des matériaux constituant la structure.

Il faut ensuite passer à la résolution des équations. Lorsque le problème étudié est de nature bi ou tridimensionnelle, il s'agit d'équations aux dérivées partielles et il est rare que les solutions exactes soient connues. Heureusement, l'apparition des ordinateurs a multiplié les possibilités de résolution d'équations aux dérivées partielles, et les solutions numériques sont aujourd'hui à la portée de la plupart des bureaux d'étude.

On peut conserver à présent un grand nombre de termes dans les représentations en série du champ des contraintes ou du champ des déplacements. On peut aussi utiliser la technique des différences finies, par laquelle l'équation différentielle est approchée à l'aide de valeurs discrètes des variables en un certain nombre de points.

Ces méthodes présentent l'avantage d'être sous-tendues par des démonstrations rigoureuses de convergence. Elles mènent souvent à des équations algébriques de forme relativement simple. L'idée de base de la méthode des éléments finis est qu'on peut représenter de manière analytique un milieu continu - l'ensemble à analyser - en le subdivisant en domaines - les éléments finis - possédant chacun ses propres fonctions pour décrire contraintes et déplacements.

On choisit la forme de ces fonctions de manière qu'elles assurent la continuité du déplacement dans l'ensemble du milieu. Si on peut exprimer le comportement de toute la structure à l'aide d'une équation différentielle unique, la méthode des éléments finis ne constitue, avec les représentations en série et les différences finies, qu'un des procédés possibles de résolution approchée de cette équation.

Mais si la structure est hétérogène, constituée d'un grand nombre de domaines répondant chacun à une équation différentielle distincte, alors seule cette méthode reste d'application directe. La méthode des éléments finis tout comme les procédés numériques en mécanique des structures, implique la formation et la résolution de systèmes d'équations algébriques. Mais les avantages qui lui sont propres résident dans l'aisance avec laquelle on peut automatiser la formation de ces équations et dans son aptitude à représenter des structures et des chargements complexes.

Les éléments finis en mécaniques sont répartis en divers types : barre simple, plaque mince chargée dans son plan, plaque mince de flexion , coque mince de révolution, coque mince gauche, élément volumique, plaque soumise à la torsion, etc.

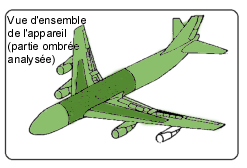
Voici un exemple simple en aéronautique. La figure montre un schéma de l'analyse par éléments finis d'une portion de Boeing 747. Le fuselage consiste en une mince enveloppe métallique ( la coque ) recouvrant une ossature formée d'une combinaison de couples et de longerons. L'armature des ailes est composée de longerons, de nervures et de raidisseurs.

L'expérience a montré que l'on peut négliger les effets des flexions locales de la coque lors de la détermination du champ global des contraintes dans une structure d'avion : on peut assimiler cette dernière à un assemblage d'éléments de contraintes planes (triangles et quadrilatères). L'ossature est idéalisée à l'aide d'éléments barre de traction-compression simple.

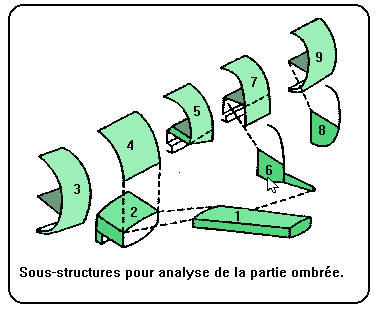
Pour analyser la région ombrée du 747, un total de plus de 7.000 inconnues a été nécessaire. La solution courante consiste à découper la structure en quelques grandes régions ou sous-structures, et à traiter chacune d'entre elles comme des super-éléments qu'il restera à assembler suivant un processus standard lors de la phase finale de l'analyse. Le tableau ci-dessous donne une idée de la complexité du problème.

Une application récente (et spectaculaire) de cette méthode de calcul est le pont suspendu du Val-Benoit au-dessus de la Meuse.

De plus en plus, les programmes de calcul par éléments finis sont à même de résoudre des problèmes de plus en plus variés (dans le même programme). Ainsi, les calculs de poutres, de coques, de transferts thermiques en régime ou transitoires, de comportements plastiques avec flambement, la cinématique des mécanismes comme les rotules, glissières, rotors avec balourd, amortisseurs, la viscoélasticité et la viscoplasticité, les champs électriques, etc.. peuvent être réalisés par la même application logicielle (comme le SAMCEF de Samtech, par exemple).

L'avantage principal des programmes généraux est surtout ergonomique : uniformité de la formation à prodiguer à leurs futurs utilisateurs, similitude des procédures d'entrée des données et d'interprétation des résultats, volume réduit de documentation nécessaire.

Les quatre phases qui sont ici regroupées en forme d'organigramme sont présentes dans quasiment tous les programmes généraux d'analyse par éléments finis.

Il s'agit de fournir les informations relatives :

Les programmes généraux les plus élaborés prévoient, par exemple, le préstockage des courbes de propriétés intrinsèques des matériaux, la décomposition de la structure en éléments finis par maillage automatique et le tracé de l'ensemble avec diverses techniques d'image de synthèse afin de permettre une détection des erreurs de données avant même le lancement de tout calcul.

C'est là que se trouvent programmés les algorithmes de formulation de tous les éléments disponibles. Cette seconde phase exploite les données entrées pour expliciter les équations algébriques des éléments à l'aide des algorithmes adéquats. Elle comprend aussi les calculs nécessaires pour déterminer la position de chaque élément par rapport à celle des éléments voisins, ainsi que les opérations permettant leur combinaison. On obtient donc un système complet d'équations algébriques relatif à la représentation en éléments finis de l'ensemble de la structure.

Cette phase traite les équations obtenues. Pour un problème d'analyse statique, cela se limitera à un système d'équations linéaires avec un second membre; par contre, un problème d'analyse en réponse dynamique exigera de vastes calculs portant sur toute l'histoire du chargement. Pour d'autres problèmes, il faudra même opérer à l'aide de sous-structures, ou effectuer des opérations spéciales sur les équations initialement construites. Cette partie comprend de plus les transformations nécessaires à l'obtention de toutes les formes désirées de la solution.

L'analyse par éléments finis fournit un document de présentation des résultats sur lequel on peut fonder des décisions concernant par exemple un choix de proportions ou d'autres questions de conception. Il s'agit classiquement d'une liste de contraintes aux sommets ou au centre de chacun des éléments, des déplacements en certains points etc... De plus en plus, les résultats sont utilisés sous forme graphiques, les images étant alors reproduites sur une imprimante thermique couleur (ou sur une table traçante à plumes ou électrostatique).

Les phases du programme général ont une caractéristique commune : la "modularité" de leurs composants. C'est-à-dire qu'un programme bien construit doit permettre à l'utilisateur d'effectuer des adjonctions ou des mises à jour d'opérations en fonction des besoins ou des améliorations possibles : par exemple ajouter des éléments, des algorithmes de résolution d'équations, des types de tracé...

Nous allons comparer au phénomène réel un modèle mathématique simple du comportement d'un élément. Ce modèle constituera une caractérisation acceptable d'un élément; disons cependant que l'approche la plus généralement empruntée ne sera pas celle que nous allons considérer ici mais procédera du point de vue des principes énergétiques et variationnels que nous développerons dans le paragraphe suivant.

Un modèle mathématique consistera à représenter l'état des contraintes (réparties sur l'ensemble des différentes régions de la structure) correspondant à des efforts - dits "forces généralisées" - qui seront localisés aux "nœuds". Les déplacements de ces nœuds suivant les degrés de liberté, suffiront à caractériser l'état déplacé de tous les éléments. La figure ci-après compare les contraintes superficielles réelles et idéalisées agissant sur la périphérie d'un élément quelconque.

On voit sur le dessin (a) que la répartition probable des contraintes est très irrégulière; il en est de même pour les déplacements non représentés. Le dessin (b) montre l'uniformité qui constitue l'idéa–lisation fondamen–tale de ce qui se produit au niveau de l'élément. Cette simplification porte sur les états des contraintes, les déformations et les déplacements. La dernière étape de l'idéalisation, dessin (c), rend l'élément plus manipulable dans l'ensemble de l'analyse : les contraintes superficielles y sont réduites à un petit nombre de forces généralisées concentrées aux nœuds. Notons que l'idéalisation fondamentale doit être telle que la représentation tende vers la réalité à mesure que l'on réduit la taille des éléments (c'est ce qu'on appelle la compatibilité).

Utilisons le problème d'analyse de la figure ci-dessus pour illustrer les raisons qui ont amené à exprimer les équations des éléments de cette façon.

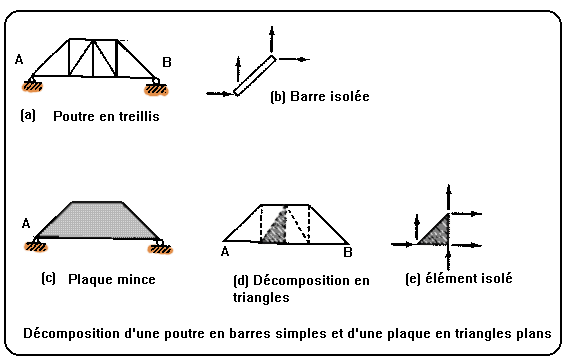
Si la poutre AB est du type du dessin (a), alors les méthodes classiques d'analyse matricielle des structures suffisent pour résoudre le problème: On isole chaque barre (dessin (b)), on exprime les relations entre forces aux noeuds et déplacements et on reconstruit analytiquement la poutre entière en exprimant l'équilibre des forces en chaque noeud.

Supposons à présent qu'il s'agisse d'une plaque mince (dessin (c)). Une décomposition semblable sera possible si la structure est représentée par un assemblage d'éléments 'plaque', des triangles comme au dessin (d). Si ces triangles sont ensuite idéalisés de la manière indiquée au dessin (e), alors une reconstruction analytique de la plaque, identique à celle de la poutre composée de barres s'en déduira immédiatement.

Cependant il faut faire quelques distinctions entre l'idéalisation de l'assemblage de barres et l'idéalisation de la plaque. Dans le premier cas, lorsqu'on effectue en chaque noeud la somme vectorielle des forces provenant des barres qui y concourent, puis qu'on écrit l'égalité des résultantes avec les charges appliquées correspondantes, les conditions d'équilibre se trouvent respectées au sein de la structure. De même, le raccordement des barres aux noeuds garantit que l'ensemble se déplace sans discontinuité géométrique.

La solution de ce problème est donc "exacte" sous l'hypothèse d'articulations parfaites ne permettant aucune flexion. Si nous avions représenté nos barres à l'aide d'un plus grand nombre d'éléments mis bout à bout, la solution serait restée la même.

Par contre, une solution par éléments finis concernant une structure continue en deux ou trois dimensions comme la plaque mince du dessin (c) ne pourra être exacte.

Afin d'illustrer la première des raisons, supposons que les éléments triangulaires du dessin (d) aient été formulés à partir des champs de déplacements pouvant varier quadratiquement sur le domaine : leurs configurations après déplacement seraient semblables à la figure ci-dessous.

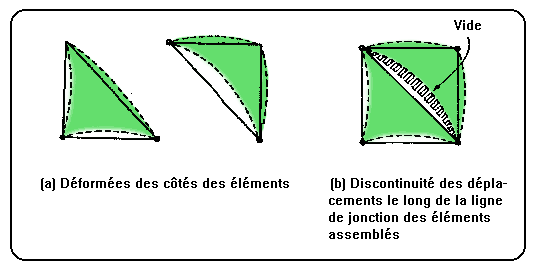
Ce qui fait qu'en général une discontinuité apparaîtra le long des frontières des éléments après assemblage comme on peut le voir à droite de la figure.

Dans ce cas la jonction par les sommets n'assurera la continuité des déplacements de la périphérie des éléments qu'en ses sommets. Une fonction quadratique doit en effet être définie par trois points pour être unique et nous n'avons utilisé pour chaque arête que les noeuds situés aux extrémités.

Remarquons que, si on augmente le nombre d'éléments comme ci-dessous, les écarts entre les déplacements des bords adjacents seront moindres et leurs effets sur la précision des résultats s'en trouveront réduits. Mais l'erreur sera de toute manière finie pour toute décomposition finie en éléments, et la solution sera toujours une solution approchée.

Il en va de même pour les conditions d'équilibre. Les forces généralisées aux noeuds sont par définition statiquement équivalentes aux efforts superficiels sur les frontières des éléments. Dans les problèmes plans ci-dessous, ces efforts ont deux composantes: Tn qui est normale à la frontière et Ts qui lui est tangente.

Supposons que les tractions normales Tn appliquées aux éléments adjacents A et B soient uniformes le long de leur frontière commune, et qu'elles soient définies de manière indépendante par certains paramètres associés aux sommets des éléments respectifs. Ces tractions différeront généralement d'un côté à l'autre de l'arête commune et les conditions d'équilibre ne seront pas respectées (le phénomène est identique pour les composantes tangentielles Ts).

On voit donc que les forces nodales ne permettent la satisfaction des conditions d'équilibres que de manière approchée. Il y a là une source d'erreur que l'on tente de réduire en affinant la décomposition à l'aide d'éléments plus petits et plus nombreux. Cette méthode ne constitue pas la seule manière de s'approcher de la solution exacte. On peut également conserver des éléments de même taille mais affiner les hypothèses sur lesquelles ils sont construits.

Les conditions d'équilibre et de continuité des déplacements sont les deux pôles des erreurs d'analyse imputables intrinsèquement à la méthode des éléments finis. La plupart des formulations tentent de respecter la continuité, et dans ce cas il faut imputer les erreurs de méthode à la non-satisfaction des conditions d'équilibre. L'ensemble des techniques de l'analyse par éléments finis permet en fait tous les dosages possibles de répartition entre ces deux sources d'erreurs.

La méthode des éléments finis est utilisée aujourd'hui de manière courante dans l'industrie pour les calculs de structures les plus variées. Son bon usage passe par la connaissance des principes théoriques fondamentaux. Le livre de Richard H. GALLAGHER, "Introduction aux éléments finis", donne à ceux qui sont amenés à utiliser la méthode, une vue unifiée des principes de base.

Il n'y a pas qu'en calcul de structure que l'ordinateur peut apporter sa puissance en simulant la réalité. Il est en fait possible de simuler à peu près n'importe quoi, pour autant que l'on aie la puissance de calcul adéquate sous la main. Ainsi, en électronique, il est de plus en plus fréquent de simuler le fonctionnement d'un circuit avant sa réalisation. De nombreux software dont certains sont gratuits ou fort bon marchépermettent la saisie du schéma avec ou sans module d'optimisation. Une liste de ces programmes se trouve ici chez un fabricant de circuits imprimés irlandais : http://www.pcb-pool.com/html_uk/uk_service_1.htm .

La possibilité est donnée à l'utilisateur d'imposer des courants et tensions alternatifs ou continus sur toutes les entrées d'un circuit. Le logiciel calcul ensuite les courants, tensions et formes d'onde en tous les points. Une fenêtre de l'écran est utilisable comme un 'oscilloscope virtuel' que l'on peut connecter n'importe où dans le circuit. Un module de paramétrisation permet de faire varier divers paramètres dans le temps de façon semi-automatique.

Le logiciel le plus connu en CAO-électronique est le programme de conception de circuits imprimés P-Cad Master Designer de la société CADAM Inc. Il permet le dessin d'un circuit de façon interactive, avec un autorouter très puissant (c'est le logiciel qui trouve par où faire passer toutes les pistes imprimées avec un minimum de 'vias', les trous métallisés). P-Cad est utilisé par plus de 20.000 personnes à ce jour.

Mais c'est en microélectronique que la CAO est la mieux implantée. En effet, il n'est plus possible du tout actuellement de réaliser un circuit intégré LSI ou VLSI 'à la main'. Seul un ordinateur est assez rapide pour loger de façon optimale les composants (transistors, diodes, conducteurs) sur un 'Die' de silicium. En microélectronique, il ne faut pas seulement faire passer des conducteurs d'un composant à l'autre, mais surtout raccourcir le plus possible les liaisons pour diminuer le 'cross-talk' et les interférences. Les liaisons passent à quelques fractions de micron au dessus des transistors Mos et l'influence capacitive ne peut pas être négligée. Les puissances de calcul demandées sont ici importantes. Le prix des systèmes de fabrication de circuit VLSI est de l'ordre de 125 Millions d’Euros pour une chaîne de montage 0.18 microns. La partie informatique intervient pour plus de 50 %  dans ce coût.

Les chimistes ne sont pas délaissés non plus et peuvent, tout comme les électroniciens, se livrer aux joies de la simulation informatisée. Dans les domaines biologiques et nucléaires, les modèles mathématiques à utiliser réservent les simulations aux superordinateurs comme les 'CRAY' et autres 'OPTION BLUE'. Mais en chimie organique ou minérale, des logiciels comme CHEM-X sur MacIntosh, offrent des performances spectaculaires.

Outre les programmes d'éléments finis, il existe des programmes plus spécifiques de simulation de mécanismes, prenant en compte les phénomènes thermiques, la lubrification, les frottements, les abrasions et ablations, etc. Certains sont à considérer comme des modules externes liés à des programmes de CAO. Quelques noms :AutoCAD (http://francais.autodesk.be) et PROEngineer (www.ptc.com), éléments finis : Samcef (www.samtech.fr).

Les valeurs numériques résultant des simulations par éléments finis ou autres méthodes peuvent être présentées sous forme de listings. Cette méthode, la plus ancienne, est aussi la plus éprouvante quand on passe à la phase de dépouillement et d'analyse des résultats. C'est pourquoi tous les programmes modernes s'efforcent de présenter leurs résultats de façon plus visuelle. Les logiciels 'tableurs' du style de Excel sont passés maîtres dans l'art de transformer des tableaux numériques en diagrammes de tous types.

Malgré cela, presque toujours, les logiciels graphiques doivent avoir une sortie graphique propre. Pour éviter les problèmes de portabilité du logiciel sur différentes types d'ordinateurs, la plupart utilisent un standard graphique tel OpenGL ou Direct3D (sous Windows) en 3D. Pour les images de synthèse de haut de gamme, le standard Renderman de Pixar (la société de Steve Jobs qui a fait Toy Story) s'impose de plus en plus. Sur le WEB, les objets graphiques sont en format GIF ou JPEG (.JPG) pour les images 2D, VRML (.WRL) pour les objets 3D

Notre propos, dans ce chapitre, n'est pas de rentrer dans les détails des méthodes d'imagerie de synthèse utilisées dans les interfaces graphiques 'CAO'. Nous verrons ceci plus en détails dans les chapitres suivants.

Remarquons que dans le cas des programmes de CAO, il ne s'agit pas de modéliser des objets pour les afficher de façon réaliste, mais bien d'afficher rapidement et clairement diverses données numériquement calculées par le système. Ainsi, un calcul de contraintes dans une pièce en volume pourra être représenté avec faces vues et cachées, chaque face étant colorée par l'effort subi par la pièce en chaque endroit de sa surface.

Bien que très utile, ce genre de technique est encore bien trop sommaire. On préférera visualiser une pièce comme un solide translucide, à travers duquel est visible une surface interne qui décrit de façon précise la position tridimensionnelle des iso-contraintes (ou plus généralement d'iso-valeurs quelconques). Diverses images de ce type, précalculées avec diverses valeurs de la contrainte à visualiser, permettent d'appréhender parfaitement les efforts en tout point du volume interne de la pièce. Dans un logiciel de visualisation interactif, il est alors possible de regarder la pièce et ses iso-contraintes de n'importe quel point de vue, en la faisant tourner sur elle-même en temps réel.

L'appréciation des déformées est un autre des aspects où l'image de synthèse n'a pas besoin de trop de réalisme. A un rendu réaliste, on préférera une représentation sommaire de l'objet déformé (en exagérant les déformations pour mieux les apprécier), pourvu qu'en même temps on puisse apercevoir le volume non déformé en semi-transparence ou en 'fil de fer'.

Les techniques informatiques d'animation peuvent toutes être utilisées pour rendre l'interface graphique plus efficace encore. On les utilisera principalement pour visualiser une série d'images précalculées représentant divers états de charge ou de vibration d'une même pièce.

Les deux usages principaux de l'animation en C.A.O. sont pourtant quelque peu 'marginaux': 'Attirer le badaud' dans les foires, congrès et expositions en est la plus remarquable. Plus sérieusement, on peut, grâce à l'animation, effectuer des présentations, éventuellement interactives, de projets à des clients ou à des décideurs non-techniciens.

Cette façon d'appréhender qualitativement les problèmes posés (et résolus) est la seule possible dans le temps forcément limité que peut prendre une présentation de projet. Il est de toute façon certain que la communication graphique, en technique comme dans bien d'autres branches, est plus efficace et plus synthétique que le langage des chiffres.

Par contre, dans le domaine des loisirs et de l’amusement, il est devenu impensable de créer des films de cinéma ou des jeux vidéo sans l’image de synthèse 3D. En région liégeoise, on trouvera par exemple les sociétés Appeal à Namur (jeux vidéo ; www.appeal.be). Dans la manipulation d'images télévisées et leur transmission, il y a la société EVS qui fabrique des serveurs pour la télévision et le cinéma digital ( www.evs.tv et www.evs-cinema.com ).

En traitement d'image pour l'industrie, il y a Euresys (www.euresys.com ).

Cette page est copyright B.Michel, 2009