| Page de Titre Table détaillée |
|
I.S.I. Gramme |
| Page de Titre Table détaillée |
|
I.S.I. Gramme |
Bitmap et vecteurs Caméra virtuelle Indépendance vis-à-vis des périphériques Bases du dessin 2D
Fonctions de manipulation 2D Bases du dessin 3D Entités graphiques 3D Fonctions 3D
Les images de synthèse sont rangées en 2 classes distinctes : les 'Bitmaps' où tous les pixels de l'image sont mémorisés et les 'Vectors' où seules sont mémorisées les définitions géométriques des objets, qui sont à chaque utilisation retransformés en bitmaps lors de l'affichage. Cette dernière méthode est bien sûr la seule qui permette des animations complexes avec mouvements de caméra, etc.
Par contre, la mémorisation de bitmaps permet d'obtenir des effets et des qualités d'image exceptionnels. En pratique, les deux méthodes sont souvent utilisées successivement et même de plus en plus intrinsèquement mélangées dans un même programme (voir les techniques de 'texture mapping').
Nous ne nous attarderons pas sur les programmes de 'Paint' qui permettent de retoucher manuellement les bitmaps. Malgré cela, n'oublions pas que ce sont des outils indispensables à l'infographiste. Le programme de ce type le plus célèbre est probablement 'Photoshop'. Depuis sa version 5.0, il gère maintenant les couleurs en 16 bits par composantes (R, G, B) permettant ainsi de rendre fidèlement 256 milliards de nuances différentes !
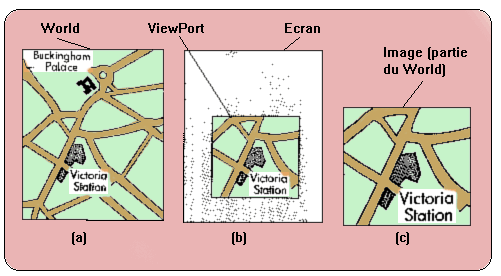
Comme en photo, l'ordinateur utilise les lois de l'optique pour réaliser des images réalistes. Nous imaginerons donc que l'écran de visualisation est une fenêtre sur laquelle on va projeter une image ou une partie de l'image du monde situé derrière lui. Si ce monde est bidimensionnel, peu de problèmes se posent. Si, par contre, comme le monde réel, le mode virtuel est en 3 dimensions, nous effectuons donc une projection des entités géométriques du monde pour en faire des entités à 2 dimensions dans le plan de l'image.
La caméra peut être considérée comme faisant partie du monde virtuel qu'elle regarde. Elle est munie de ses paramètres propres comme la position, l'ouverture, l'orientation, etc. Cette façon de considérer le système permet au programmeur de manipuler les points de vue en ne modifiant en rien la géométrie du monde observé, et aussi de modifier un élément de ce monde sans perturber le point de vue.
Un programme d'animation en images de synthèse se résume donc à une structure de ce genre :
· Créer le monde immobile (le décor fixe)
· Créer les objets mobiles (le reste)
· Définir la caméra
· Boucle à effectuer pour toutes les images :
modifier la géométrie des objets mobiles
modifier les paramètres de la caméra
calculer une image
· Fin
Même dans un monde à deux dimensions, on doit pouvoir ne visualiser qu'une partie du monde. On associera à la caméra une 'taille de fenêtre' qui indique quelle portion du monde est vue.
Nous supposerons que, dans notre monde à 2 ou 3 dimensions, les coordonnées des entités qui le composent sont décrites par des nombres flottants. Les limites du monde sont donc vastes (par exemple de +2.000.000 à -2.000.000 dans chaque direction). Les dimensions et la position de la fenêtre de visualisation sont aussi données dans ces mêmes coordonnées.
En 2 dimensions, il suffit de préciser les cordonnées du centre de la fenêtre, sa hauteur et sa largeur (4 nombres). En 3 dimensions, nous devons donner plus de renseignements. Ainsi, on peut, par exemple, décrire une caméra par sa position (3 nombres), sonangle d'ouverture (1 nombre) et son orientation (2 ou 3 nombres). Cette dernière sera le plus souvent remplacée par les coordonnées (3 nombres) d'une cible située à une distance quelconque sur l'axe de la caméra. On peut malgré tout indiquer une dernière rotation : celle de la caméra autour de son axe propre.
Pour s'y retrouver plus aisément, on dit que l'on fait tourner le 'UP-VECTOR' autour de l'axe de visé. on appelle. UP-VECTOR le vecteur vertical situé dans le plan de la caméra.
Pour éviter de devoir modifier profondément le logiciel pour l'adapter à divers types d'écran, de tables traçantes ou d'imprimantes, nous effectuons nos opérations de fenêtrage en 2 temps. Tous nos calculs vont ramener les coordonnées des objets du monde virtuel (les WC -World Coordinates) en coordonnées NDC (Normalised Device Coordinates) qui vont usuellement de 0.0 à +1.0 dans les deux directions X et Y. En dernier lieu, le DEVICE DRIVER ou programme de sortie, affichera nos entités géométriques dans le système de coordonnées réel du périphérique de sortie (les DC - Device Coordinates), par exemple pour les fenêtres de taille variable des systèmes multifenêtres comme Windows, MacOS, X-Windows, BEos, etc.
Conventions usuelles pour les axes
En 2D, du point de vue de la caméra, X va de gauche à droite dans le sens positif Y va de bas en haut dans le sens positif. |
En 3D, du point de vue de la caméra, X va de gauche à droite dans le sens positif Y va de bas en haut dans le sens positif Z est tel que l'observateur regarde dans la direction des Z négatifs. Les Z positifs s'étendent donc vers l'arrière (la partie invisible) de l'image. |
Règle de la main droite : Ecrivez un X sur l’ongle de votre pouce droit, un Y sur celui de votre index droit et Z sur celui de votre majeur droit. Mettant ces 3 doigts en trièdre, vous obtenez un système d’axe comme celui décrit ci-dessus, dit aussi trièdre dextrogyre.
En ce qui concerne les périphériques, les axes en coordonnées DC sont souvent définis avec l'axe vertical inversé (cas du PC et de la plupart des micro-ordinateurs).
Le terme Window désigne l'ensemble de paramètres permettant de transformer notre monde virtuel de ses coordonnées WC en coordonnées NDC. Ceci comprend principalement la définition de caméra virtuelle (en WC).
Le ViewPort est, lui, défini en coordonnées NDC et spécifie à quelle portion de l'écran doit correspondre l'image obtenue. Le cas simple où l'image occupe tout l'écran n'est pas le seul! Presque tous les programmes graphiques utilisent au moins une partie de l'écran pour des menus, d'autres vues, des zones de saisie de texte.
La procédure d'affichage d'un monde 3D se résume donc à :
· Projection 3D-2D de la fenêtre (window) en WC.
· Transformation des coordonnées WC de la fenêtre en coordonnées NDC du viewport.
· Transformation des coordonnées NDC du viewport en coordonnées DC du périphérique par le Device Driver.
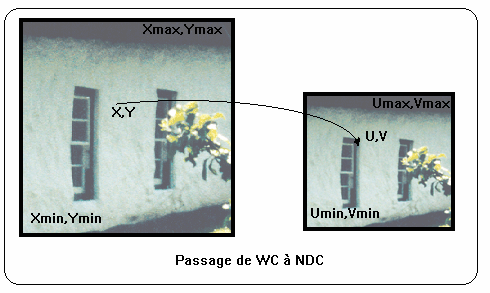
Le problème de transformation se résume donc à transformer les coordonnées WC (x1, y1) et (x2, y2) des extrémités d'un segment de droite en coordonnées NDC (u1, v1) et (u2, v2). Sachant que la fenêtre ouverte sur le monde (WC) a pour coin inférieur gauche le point (Xmin, Ymin) et pour coin supérieur droit le point (Xmax, Ymax), nous pouvons faire une simple règle de trois :
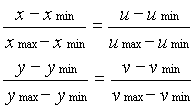
que nous pouvons résoudre pour trouver les valeurs de u et v :
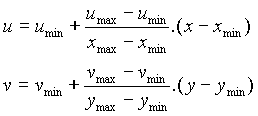
Chaque point d'une ligne ou d'une courbe doit être transformé de cette façon. De même, les coordonnées NDC seront transformée par une procédure similaire en coordonnées DC avant affichage. Nous remarquons tout de suite qu'un problème peut se poser : si le point calculé in fine se trouve hors du viewport, seule une partie de notre segment sera affiché. C'est la procédure de clipping que nous étudierons plus loin..
Les instructions de base disponibles dans le langage informatique ou dans la bibliothèque graphique peuvent varier. Dans tous les cas, si elles n'existent pas ou ne nous conviennent pas, il nous faudra les réécrire. Pour les périphériques du type 'table traçante' et aussi pour les tracés à l'écran, voici quelques primitives de tracé très utiles (inspirées du standard GKS) :
line(x1,x2,y1,y2) |
Trace une ligne de (x1,y1) au point (x2,y2). |
line_to(x,y) |
Trace une ligne de la position courante (PC) au point (x,y). |
move_to(x,y) |
Déplace la position courante (PC) en (x,y). |
line_rel(dx,dy) |
Trace une ligne de la position courante (PC) au point (PCx+dx,PCy+dy). |
move_rel(dx,dy) |
Déplace la position courante (PC) au point (PCx+dx,PCy+dy). |
On notera l'usage de la position courante PC qui constitue un 'curseur' mémorisé par les routines graphiques. Dans certaines librairies graphiques, il est possible d'utiliser plusieurs curseurs simultanément.
Dans certains langages (LOGO, Draw du Basic IBM), on trouve aussi des 'Turtle graphics' qui sont des descriptions de trajectoires vues du point de vue du curseur. Par exemple : avancer de 3, tourner à gauche de 45°, lever la plume, avancer de 4, baisser la plume, etc. Ce type d'implémentation est très utile en 2 D, par exemple pour le tracé des chaînes de caractères mémorisées sous forme vectorielle. Dans le programme AutoCAD, les fontes 'SHAPES' sont créées de cette façon. Il est très aisé de tracer des caractères de différentes tailles et dans n'importe quelle orientation avec ce type d'instructions.
Les points sont définis (en coordonnées WC) comme deux nombres x et y. Dans quasi tous les programmes, ce sont des nombres flottants. Certains préfèrent travailler en nombres entiers, mais ceci pose de nombreux problèmes de précision pour les objets de petite taille (la moitié de 3, en nombre entiers, c'est quoi ???). On élimine partiellement cet inconvénient en travaillant dans un monde de taille limitée, où aucun objet ne peut être trop petit. Par exemple, un monde de 32000 x 32000 points et des objets de taille comprises entre 100 et 1000 points offre déjà pas mal de possibilités.
Un point P contient deux valeurs flottantes :
P.x et P.y
Nous utilisons ici une notation inspirée du langage C, où une structure de données porte un nom (ici P) et un élément de cette structure est désigné par le nom de la structure, un point et le nom générique de la zone concernée(ici P.x).
La structure d'un point 2D est donc :
struct Point { float x;
float y;
}
En 3 dimensions, nous étendrons la notion de point à la troisième coordonnée z :
struct Point { float x;
float y;
float z;
}
Les vecteurs représentent des directions ou des déplacements relatifs. Ils sont représentés de façon identique aux points. Bien qu'ils désignent une réalité physique différente, ils utilisent les mêmes structures de données que les points.
On utilisera très souvent des vecteurs normés, c'est-à-dire des vecteurs ramenés à une longueur unitaire. En effet par exemple, pour comparer deux directions identiques P et Q, la simple comparaison de P.x avec Q.x, etc. ne serait pas satisfaite si un des vecteurs a une longueur double de l'autre. Pour normer un vecteur, il faut diviser ses composantes par la longueur du vecteur (et faire attention au risque de division par zéro!).
P_normalised.x = P.x/L
P_normalised.y = P.y/L
P_normalised.z = P.z/L
En conjonction avec un point, un vecteur peut servir à représenter un segment de droite. Il est en effet très facile de tracer un segment de droite à partir de son origine P0 (point) dans la direction V (vecteur). Pour cela, on utilise l'équation paramétrique vectorielle du segment :
P(a)=P0+a*V où a est un paramètre variant de 0 à 1,
P0 un point et V un vecteur de longueur égale à celle du segment
Les courbes ne peuvent pas, pour nous, être représentées par des équations du type y = f(x) car ce type de représentation est souvent incomplet ou pose des problèmes d'algorithmes.
La simple ligne droite ![]()
nous pose déjà un problème. Le cas de la droite verticale est mieux décrit par x = Cste que par l'équation ci-dessus, où le paramètre a vaut l'infini et où la solution de l'équation est indéterminée.
Quant au cercle, ![]()
est l'équation du demi-cercle supérieur et non du cercle complet. Il nous faut donc 2 équations pour représenter le cercle complet.
Tournons nous donc vers la représentation implicite des équations définissant une courbe. L'équation d'une droite quelconque sera donnée par :
![]()
On peut montrer que la distance entre la droite et l'origine des axes est :
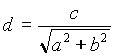
si l'équation de la droite est normalisée (c'est-à-dire que a, b et c sont tels que a2+b2=1), la distance entre la droite et l'origine des axes est :
![]()
Remarquons que la ligne en tant que telle ne nous intéresse pas. Ce qui nous intéresse, c'est de tracer des segments de droite. Donc, nous allons expliciter l'équation implicite de la droite en fonction de deux de ses points qui sont les extrémités d'un segment (x1, y1) et (x2, y2). On obtient finalement :
![]()
Cette représentation est la plus utile. Elle permet de retrouver très facilement l'équation d'une droite passant par deux points.
En 2D, on peut représenter une courbe par 2 équations explicites pour une variable appelée le paramètre.Une courbe en deux dimensions sera représentée par :
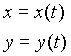
Bien sûr, il n'y a aucun problème à extrapoler cette représentation aux trois dimensions si nécessaire :
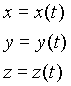
Usuellement, le paramètre variera d'une valeur 0 à une extrémité du segment de courbe
qui nous intéresse à une valeur 1 pour l'autre extrémité. Ainsi, le segment de droite
reliant les points (x1, y1) et (x2, y2) sera représenté par :
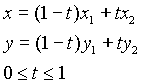
Cette forme permet de vérifier facilement l'intersection entre deux segments de droite du plan. Soit un second segment de droite représenté comme ceci :
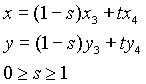
Le point d'intersection est obtenu en égalant les membres de gauche des deux groupes d'équations ci-dessus. On obtient :
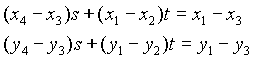
Si les droites ne sont pas parallèle, il existe une solution pour s et pour t. Si de plus , s et t sont tous les deux compris entre 0 et 1, c'est que les segment se coupent.
Une courbe de Bézier ( http://moshplant.com/direct-or/bezier/index.html )est une courbe paramétrique définie par 4 points (P1, P2, P3 et P4). Elle commence au point P1 et se termine au point P4. Sa direction à l'origine (t=0) est celle du vecteur P1-P2 et sa direction à l'extrémité (t=1) est celle de P3 - P4. Les coordonnées d'un courbe de Bézier sont données par l'équation paramétrique suivante :
![]()
ou encore :
![]()
et de même pour y (et pour z en 3 dimensions). On vérifie facilement que pour t = 0, on a bien x = P1x et que pour t = 1, on a bien x = P4x.
On peut vérifier facilement que le long de deux courbes de Bézier consécutives a et b (P1b = P4a), la courbure est constante à la jonction si les vecteurs terminaux sont égaux (P2b-P1b = P4a - P3a). On peut ainsi approximer une courbe quelconque par une suite de Bézier répondant à cette condition. Le vecteur à chaque jonction indique la direction de la tangente en ce point, et sa longueur est inversement proportionnelle à la courbure de la courbe.
Une courbe complexe constituée de segments de Bézier est en anglais une Piece-Wise Polynomial Curve. Cette courbe est continue si et seulement si les vecteurs terminaux de deux segments successifs sont égaux et opposés.
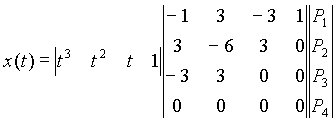
Une propriété intéressante des polynômes de Bézier est que toute la courbe (pour 0<t<1) est comprise à l'intérieur du polynôme convexe formé par les 4 points de contrôle. En effet, les coordonnées d'un point sont données par une combinaison linéaire des coordonnées des 4 points affectées d'un coefficient inférieur à 1. Cette propriété est utilisée pour déterminer à priori si une courbe de Bézier risque d'intersecter une autre entité géométrique, et particulièrement le bord d'une Window ou d'un Viewport (voir le problème du clipping).
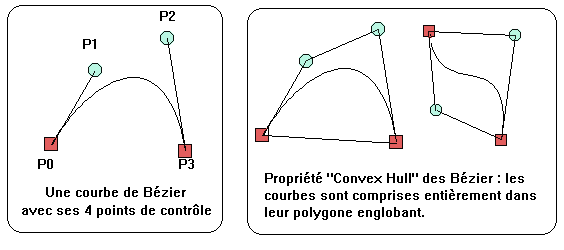
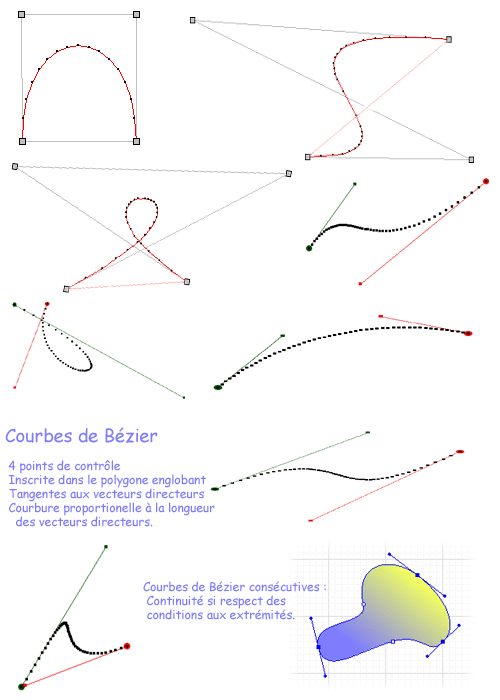
On a vu que les courbes de Bézier n'ont une continuité de courbure que si on leur impose une condition supplémentaire sur la position des points de contrôle. D'autre part, nous ne voulons pas augmenter l'ordre des polynômes utilisés, car le temps de calcul en souffrirait trop et on perdrait l'avantage de 'localité' des paramètres. En effet, avec les Bézier, seuls quatre points influencent la génération d'un élément de courbe. En gardant ces avantages, et en imposant la continuité des dérivées premières et secondes, on arrive à l'emploi d'autres courbes d'ordre trois : les Splines.
Considérons une courbe définie par une succession de points. Nous allons générer un petit élément de courbe entre les points k et k+1. Pour définir une cubique, il nous faut quatre conditions indépendantes. Nous prendrons donc les coordonnées de quatre points consécutifs, les points k-1, k, k+1 et k+2.
Il s'agit toujours de courbes paramétriques. Le paramètre t varie de 0 à 1 et on a judicieusement choisi les coefficients des équations pour qu'elles restent symétriques par rapport au paramètre.Nous donnons ici les équation définissant la coordonnée x. Il est évident qu'il en va de même pour y (et pour z en 3 dimensions).
![]()
avec :
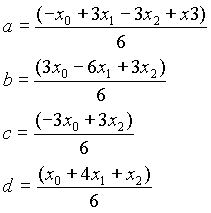
Un courbe Spline ainsi définie est bien symétrique par rapport à t dans l'intervalle 0-1. On voit en effet que pour t=0 :
![]()
et que pour t=1 :
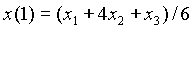
Les Splines, comme les Bézier, vérifient la condition (convex hull) que toute la courbe (pour 0<t<1) est comprise à l'intérieur du polynôme convexe formé par les 4 points de contrôle. En effet, les coordonnées d'un point sont données par une combinaison linéaire des coordonnées des 4 points de contrôle affectées d'un coefficient inférieur ou égal à 1.
Les Splines assurent la continuité des dérivées première et seconde, ce qui donne à la courbe un aspect très lisse et 'coulé' (smooth). Mais, au rayon des inconvénients, on peut citer le fait que les Splines ne passent généralement par aucun de leurs points de contrôle et qu'elles nécessitent trois fois plus de calculs que les Bézier équivalentes.
Ceci se constate aisément en regardant les deux types de courbes. Une seule courbe de Bézier se base sur quatre points successifs, tandis que la Spline se basant sur les mêmes points n'occupe que le tiers central de cet élément de courbe. Elle commence près du second point de contrôle et se termine près du troisième.
Suivant les valeurs des paramètres a, b, c et d, les splines ont diverses représentations et diverses propriétés. On utilise le plus couramment les courbes C-Splines et B-Splines, dont les matrices de définition sont reprises ci-dessous.
![]()
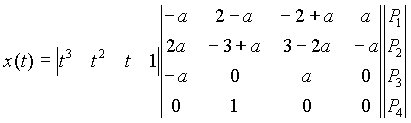
Représentation matricielle d'une courbe Spline générale en 3 dimensions
Les coefficients de la matrice des splines cardinaux sont exprimés en fonction du
paramètre a appelé 'tension'. La valeur la plus courante de la tension est 1/2,
ce qui donne lieu à l'existence des 'Cardinal Splines' ou C-Splines.
Diverses manipulations mathématiques doivent être effectuées sur les figures 2D. Les rotations et autres transformations matricielles sont en général appliquées aux points 3D avant projection dans le plan de l'écran.
Mais, il existe trois fonctions de manipulations 2D très importantes : l'intersection d'un segment de droite avec les bords du viewport (clipping), le tracé de segments de droite lui-même et le remplissage de surfaces (Fill) qui est aussi un problème délicat.
Pourquoi nous préoccuper de ces problèmes ? Tous les langages informatiques ont des fonctions 'line' et 'fill' qui effectuent ces tâches parfaitement. Mais... nous n'avons dans ce cas plus aucune maîtrise sur la manière dont la ligne est tracée. Si nous voulons antialiaser (voir plus loin) un segment de droite, nous sommes obligés de le tracer point par point avec notre algorithme particulier.
De même pour remplir une surface, nous ne pouvons pas utiliser l'instruction 'fill' de notre carte graphique si nous voulons appliquer des textures ou des rendus spéciaux comme le Gouraud ou le Ray Tracing.
Le but du clipping est de déterminer quelle partie d'un objet appartient à la fenêtre d'affichage. On peut tout d'abord calculer si l'objet à afficher est entièrement dans la fenêtre ou entièrement en dehors. Si ce n'est aucun de ces deux cas, c'est que l'objet doit être partiellement affiché. Il faut donc couper les segments de droite (ou de courbes) qui le composent exactement à la frontière de la fenêtre d'affichage.
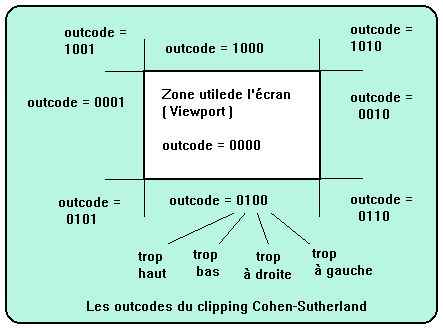
Le but du procédé de clipping décrit ici est donc de couper un segment de droite pour en conserver la partie visible dans le viewport. L'espace entourant le viewport est séparé en 8 zones à l'appellation binaire bien précise.
Les 9 zones sont repérées par 4 bits. Ces nombres sont appelés 'outcodes'. Le bit 0 indique 'trop à gauche', le bit 1 indique 'trop à droite', le bit 2 indique 'trop bas' et le bit 3 'trop haut'. Les 4 bits à zéro indiquent que l'on est bien dans la partie visible.
On commence par calculer l'outcode à chaque extrémité du segment à couper.
Soit A (x, y) une de ces extrémités et xmin, xmax, ymin et ymax les coordonnées des côtés du viewport :
puis, on traite le segment pour n'en garder que la partie montrable :
si(outcode(A) OR outcode(B) = 0) afficher
tout. (si A et B valent tous deux 0000)
si (outcode(A) AND outcode(B) <> 0) ne pas afficher. (si au moins 1 bit commun
existe)
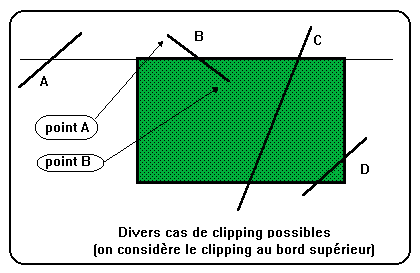
Ici, ne nous restent plus que les segments partiellement visibles (voir figure ci-contre).
Si A est visible dans le viewport, inversons A et B :
si (outcode(A) = 0) inverser (A,B)
Supposons que le point A est au dessus de l'image. La résolution du problème resterait similaire s'il s'agissait d'un autre côté.
Calculons l'intersection C du bord supérieur (y=ymax) avec notre segment et remplaçons A par ce point.
Cy = Ymax intersection avec y=ymax
Cx = Ax + (Bx-Ax) * (ymax-Ay)/(By-Ay)
Ax = Cx remplacer A par C
Ay = Cy
Le but de cet algorithme est d'allumer des points de l'écran pour tracer un segment de droite en allumant les pixels nécessaires ni plus ni moins, et en utilisant au mieux le processeur. On préfère exécuter des comparaisons ou des incrémentations plutôt que des multiplications. De plus les coordonnées en pixels sont forcément des nombres entiers, ce qui pose divers problèmes d'arrondi.
On constate tout d'abord que le problème est symétrique en x et y. On peut donc toujours le ramener au cas où la pente de la droite est comprise entre 0 et 1(1er demi-quadrant).
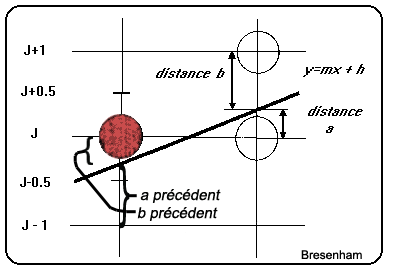
Supposons que le pixel (i, j) vient d'être allumé et que la droite est donnée par l'équation :
![]()
Le point (i, j) n'était probablement pas exactement sur la droite, puisque i et j sont des nombres entiers. On peut donc dire que sur la verticale x = i , on a :
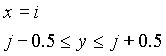
Le pixel suivant à allumer est sur la verticale x = i + 1. Il y donc deux possibilités, puisque la pente est inférieure à 1 : y vaut soit j, soit j + 1. Sur la figure de droite ci-dessus, on se servira des distance a et b pour effectuer le choix. Le problème est donc réduit à déterminer les valeurs successives de a et de b. Le segment étant donné au départ par ses extrémités (x1,y1) et (x2,y2), la pente de droite est donc :
![]()
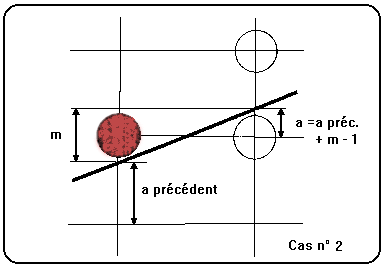
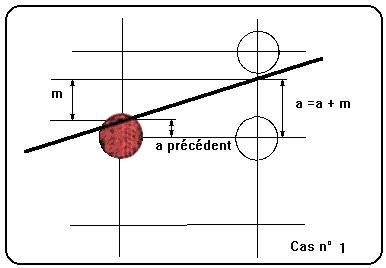
A chaque pas horizontal où x augmente de 1, y augmente donc de la valeur m. La distance a qui nous intéresse est incrémentée de m si x seul a changé, ou de m - 1 si x et y ont été tous deux incrémentés au pas précédent (voir figures ci-contre).
De même, la distance b variera de -m ou de 1-m suivant les cas. Comme la variable sur laquelle se base notre décision est (a - b), on peut trouver la nouvelle valeur de (a - b) à partir de l'ancienne en y ajoutant soit 2m, soit (2m - 2). Pour réduire encore notre algorithme, remarquons que seul le signe de (a - b) nous intéresse, et non sa valeur (qui, de plus, est un nombre flottant et donc à priori lent à calculer).
On peut donc multiplier (a - b) par une constante sans modifier le résultat de notre test. Choisissons comme constante la valeur (x2 - x1). notre 'variable de décision' devient donc soit e = 2 m (x2-x1), soit e = 2 (m - 1) (x2-x1), valeurs que l'on peut réduire à e = 2 (y2 - y1) et e = 2 (y2 - y1 - x2 + x1). La base de notre algorithme est donc :
Valeurs initiales :
inc1 = 2(y2 - y1)
inc2 = 2(y2 - y1 - x2 + x1)
e = 2(y2 - y1)-(x2 - x1)
A chaque pixel :
si (e>0) (
e = e + inc1
y = j
)
sinon (
e = e + inc2
y = j + 1
)
x = i
set_pixel (i,j)
L'algorithme complet s'occupe aussi des droites dont la pente est supérieure à 1 en inversant les rôles de x et de y, et de celles dont la pente est négative par symétrie. Voici le listing complet de son implémentation en langage 'C' :
typedef struct /* on définit la structure */
{ /* d'un point */
float x;
float y;
}point
void Bresenham(x1,y1,x2,y2)
int x1,x2,y1,y2;
{
int dx,dy,i,e,incx,incy,inc1,inc2,x,y;
point location;
dx = x2 - x1 ; dy = y2 - y1;
if (dx<0) dx=-dx;
if (dy<0) dy=-dy;
incx=1 ; if (x2<x1) incx=-1;
incy=1 ; if (y2<y1) incy=-1;
x=x1;y=y1;
if (dx<dy)
{
location.x=x;location.y=y;
set_pixel(&location);
e=2*dy-dx;
inc1=2*(dy-dx);inc2=2*dy;
for(i=0;i<dx;i++) /*boucle exécutée dx fois */
{
if (e>=0)
{
y+=incy;
e+=inc1;
}
else e+=inc2;
x+=incx;
location.x=x;location.y=y;
set_pixel(&location);
}
}
else
{
location.x=x;location.y=y;
set_pixel(&location);
e=2*dx-dy;
inc1=2*(dx-dy);;inc2=2*dx;
for(i=0;i<dy;i++) /*boucle exécutée dy fois */
{
if(e>=0)
{
x+=incx;
e+=inc1;
}
else e+=inc2;
y+=incy;
location.x=x;location.y=y;
set_pixel(&location);
}
}
}
La routine set_pixel peut simplement allumer un point de l'écran mais peut aussi être bien plus complexe, prenant en compte des types de lignes (pointillés, traits d'axe,...) ou diverses couleurs ou variations de couleurs.
L'algorithme récursif de Smith est utilisé pour remplir des zones de forme quelconque dans un bitmap.
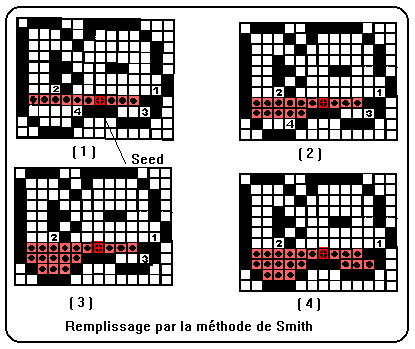
Il utilise une méthode qui traite la zone à remplir en la regardant comme une série de segments horizontaux. On part d'un point quelconque situé dans la zone à remplir (le 'seed' ou graine en anglais) et on trace jusqu'aux deux bords gauche et droit de la zone des segments.
Une fois un segment tracé, on examine les segments situés au-dessus et au-dessous et on mémorise dans une pile les coordonnées des extrémités droites des segments encore à remplir. Ceux-ci servent à leur tour de point de départ, et l'algorithme se termine quand la pile est vide. Sur les dessins, les numéros indiquent dans quel ordre les points ont été empilés.
Il existe deux façons de représenter des objets 3D : la méthode volumique (CSG) et la méthode surfacique (B-Rep).
La méthode volumique, ou CSG (constructive solid geometry) se base sur l'addition ou la suppression de volumes élémentaires simples. Exemple : prendre un cylindre, ajouter un cube, soustraire une sphère, etc.
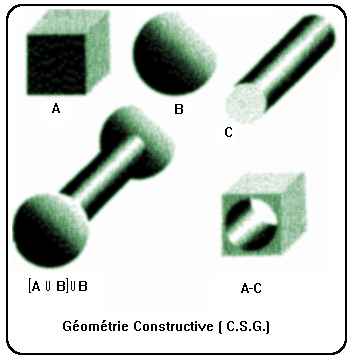
Pour les volumes complexes, la méthode CSG décompose l'espace en cubes élémentaires.
Cette méthode permet de représenter des volumes très complexes, mais est une très grande consommatrice de mémoire. Une des méthode CSG les plus connues est celle des 'octree' qui décompose un espace cubique en 8 cubes élémentaires. Si un de ces cubes est entièrement plein ou entièrement vide, on le mémorise comme tel. Sinon, on le décompose en 8 autres cubes plus petits et on reprend le processus récursivement jusqu'à obtenir la précision voulue. Le volume des données est tout à fait impressionnant !
La figure ci-dessous et celle de la page précédente montrent comment on peut assembler un volume par addition ou par soustraction de volumes plus simples. Les opérations booléennes classiques sont applicables, telles que union, intersection, différence.
La méthode surfacique mémorise uniquement des surfaces dans l'espace. Ce sont les surfaces qui entourent l'objet. 'B-rep' signifie Boundary-representation ou description par les frontières. Cette méthode est de loin la plus utilisée, car elle est bien moins vorace en temps de calcul et en espace mémoire. Par contre, elle pose des problèmes lors du maillage tridimensionnel demandé par les méthodes d'éléments finis, par exemple. Heureusement ces problèmes ne sont pas insurmontables.
La méthode surfacique mémorise uniquement des surfaces dans l'espace. 'B-rep' signi–fie Boundary-representation pou description par les frontières. Cette méthode est de loin la plus utilisée, car elle est bien moins vorace en temps de calcul et en espace mémoire. Par contre, elle pose des problèmes lors du maillage tridimensionnel demandé par les méthodes d'éléments finis, par exemple. Heureusement ces problèmes ne sont pas insurmontables.
Les trois entités de base en 3D sont le point, le segment de droite et la facette. Un point est défini par ses 3 coordonnées x, y et z. Le segment de droite est défini par les deux points situés à ses extrémités. La facette est supposée plane et est définie par les points qui sont à ses sommets. Leur nombre peut être quelconque, mais de nombreux programmes ne travaillent qu'avec des facettes triangulaires (fatalement toujours planes) ou quadrangulaires.
Les volumes plus complexes sont quasi toujours représentés par un certain nombre de ces facettes. Certains volumes simples ont toutefois une plus grande importance.
La boîte (box en anglais) est un parallélépipède rectangle aligné sur les axes du monde. Elle peut donc être définie par les coordonnées de son centre et sa taille en x, y et z, soit six valeurs numériques. Elle est très utile car il est fort facile de tester si un point, un segment ou une facette est dans la boîte ou dehors.
La sphère est aussi très importante. On ne la dessine pas souvent, mais on s'en sert car un point situé dans une sphère de centre A et de rayon R est forcément à une distance inférieure à R du point A.
Dans la plupart des programmes professionnels, et même dans les cartes graphiques des ordinateurs, les données sont manipulées sous forme de vecteurs et de matrices de transformation. La complexité des méthodes matricielles est telle qu'elle déborde du cadre de ce cours. Il faut dons garder à l'esprit que les fonctions décrites ici ne sont pas les plus efficaces, car nous n'y incluons pas toute une série d'astuces comme la combinaison de matrices en coordonnées homogènes, etc.
Il est nécessaire de disposer d'un grand nombre de fonctions de base pour manipuler des coordonnées en 3D. En voici quelques-unes.
On notera que les définitions d'un vecteur et d'un point sont identiques. La différence entre deux points donne le vecteur direction du premier point vers le second.
Soit les vecteurs A et B (Ax, Ay, Az) et (Bx, By, Bz) ,S leur somme et D leur différence :
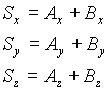
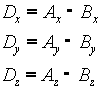
Soit les points A et B (Ax, Ay, Az) et (Bx, By, Bz) :
![]()
Soit le vecteur A (Ax, Ay, Az) :
D = Distance (point_A, point_B)
Si D = 0, erreur (il faut éviter les divisions par zéro)
Ax = Ax / D
By = Ay / D
Az = Az / D
Cette fonction sert à changer la longueur d'un segment. Appliquée à un vecteur unitaire, elle lui donne une longueur connue.
Soit le vecteur A (Ax, Ay, Az) et le scalaire L :
Ax = Ax * L
By = Ay * L
Az = Az * L
Le cosinus de l'angle entre deux vecteurs est donné par le produit de ces deux vecteurs, pour autant qu'ils soient normés. L'angle entre la normale à une surface et un rayon de lumière incident est nécessaire dans tous les calculs de rendu (Gouraud, Phong, Ray tracing, etc...)
Soit le vecteur A (Ax, Ay, Az), le vecteur B (Bx, By, Bz) et l'angle Alpha entre eux :
Normaliser (A)
Normaliser (B)
Prod = Ax * Bx + Ay * By + Az * Az
Alpha = arcos (Prod)
Le produit vectoriel de deux vecteurs donne un vecteur perpendiculaire au plan constitué par les deux vecteurs de départ.
Soit les vecteurs A (Ax, Ay, Az) et B (Bx, By, Bz) et le produit vectoriel P (Px, Py, Pz) :
Px = (Ay * Bz) - (By * Az)
Py = (Bx * Az) - (Ax * Bz)
Pz = (Ax * By) - (Bx * Ay)
Un plan est défini par les quatre coefficients a, b, c et d de son équation (ax + by + cz + d = 0). Pour faciliter la comparaison entre deux plans, on normalise toujours ces quatre valeurs. C'est-à-dire que l'on s'arrange pour que :
![]()
L'orientation du plan dépend de l'ordre dans lequel les points sont donnés. Par convention, on donne les points dans l'ordre inverse des aiguilles d'une montre quand le plan est regardé par le côté visible (l'extérieur de l'objet). cette propriété est utilisée pour les tests de visibilité (vu-caché).
Si cette notion n'est pas utilisée, il faut lever l'ambiguïté de l'algorithme ci-dessous en imposant au coefficient a d'être positif ou nul (si a est nul, on impose b positif ou nul, etc..) pour obtenir une équation véritablement unique pour un plan donné.
On notera aussi que le vecteur unitaire (a, b, c) est perpendiculaire au plan. C'est la NORMALE du plan. Autre rappel de géométrie : en remplaçant dans l'équation du plan les inconnues x, y et z par les coordonnées d'un point, on obtient comme valeur du polynôme la distance du point au plan (et donc zéro si le point est dans le plan).
Le signe de cette distance indique de quel côté du plan le point se situe.
Soit trois points non alignés A (Ax, Ay, Az), B (Bx, By, Bz) et C (Cx, Cy, Cz) et le plan P (Pa, Pb, Pc, Pd) :
Pa =
(Ay*Bz)+(By*Az)+(Az*Cy)-(Bz*Cy)-(Az*By)-(Ay*Cz)
Pb = (Az*Bx)+(Bz*Cx)+(Ax*Cz)-(Bx*Cz)-(Ax*Bz)-(Az*Cx)
Pc = (Ax*By)+(Bx*Cy)+(Ay*Cx)-(By*Cx)-(Ay*Bx)-(Ax*Cy)
Pd = -(Ax*By*Cz)-(Az*Bx*Cy)-(Ay*Bz*Cx)+(Az*By*Cx)+(Ay*Bx*Cz)+(Ax*Bz*Cy)
L = SQR(Pa2 + Pb2 + Pc2)
Pa = Pa / L
Pb = Pb / L
Pc = Pc / L (Ceci est le plan normalisé donné par ses 4 composantes)
Pd = Pd / L
Cette fonction découle directement de l'équation du plan décrite ci-dessus.
Soit le point A (Ax, Ay, Az) et le plan P (Pa, Pb, Pc, Pd) et la distance D :
D(point_A, Plan_P) = (Pa* Ax) + (Pb*Ay) + (Pc*Az) + Pd
Avant d'effectuer une rotation, une symétrie ou un changement d'échelle autour d'un point donné, il faut d'abord déplacer l'origine des axes au centre de transformation. Après la transformation, on fait subir aux points concernés la translation inverse.
Ceci équivaut à déplacer l'objet à transformer à l'origine, y effectuer la transformation, puis ramener l'objet à sa place.
Pour effectuer la translation, on soustrait des coordonnées de l'objet celles du centre de transformation R. Ceci équivaut à faire subir à l'objet une translation égale au vecteur (origine des axes - R)
Soit le point A (Ax, Ay, Az) et le centre de transformation R (Rx, Ry, Rxz) :
Ax = Ax - Rx
Ay = Ay - Ry
Az = Az - Rz
Effectuer une rotation autour d'un axe n'affecte évidemment pas la coordonnée des points le long de cet axe. Ainsi, une rotation autour de l'axe Z ne modifie que les coordonnées x et y. La rotation est en fait la multiplication du vecteur 'coordonnée du point' par une matrice unitaire de rotation. Le vecteur résultant est le point déplacé.
Soit le point A (Ax, Ay, Az) et l'angle Alpha de rotation autour de l'axe z :
A'x = Ax * Cos(Alpha) - Ay * Sin(Alpha)
A'y = Ax * Sin(Alpha) + Ay * Cos(Alpha)
A'z = Az
Soit le point A (Ax, Ay, Az) et l'angle Alpha de rotation autour de l'axe x :
A'x = Ax
A'y = Ay * Cos(Alpha) + Az * Sin(Alpha)
A'z = - Ay * Sin(Alpha) + Az * Cos(Alpha)
Soit le point A (Ax, Ay, Az) et l'angle Alpha de rotation autour de l'axe y :
A'x = Ax * Cos(Alpha) - Az * Sin(Alpha)
A'y = Ay
A'z = Ax * Sin(Alpha) + Az * Cos(Alpha)
Il est évident que par souci d'efficacité, il convient de pré-calculer les sinus et cosinus en dehors de la boucle qui applique la transformation à tous les points d'un objet, donc pour faire tourner un groupe de points autour de l'axe z :
C = Cos(Alpha)
S = Sin(Alpha)
Boucle (Ai = A0 à An)
A'ix = Aix *
C - Aiy * S
A'iy = Aix *
S + Aiy * C
A'iz = Aiz
fin de boucle
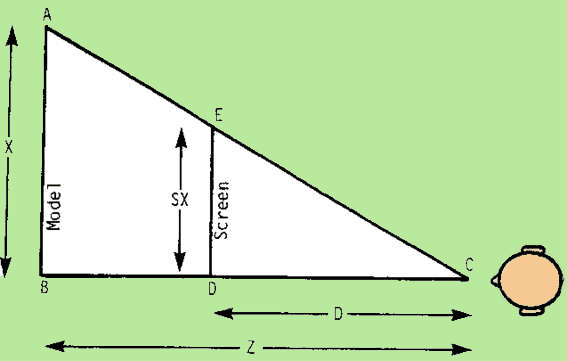
A un moment donné du processus, notre image à 3 dimensions doit devenir plane. Ceci s'effectue par l'opération de projection. On suppose toujours la caméra située à l'origine et regardant dans la direction z.
L'opération de projection est une simple règle de trois, comme on peut le voir sur la figure ci-dessus.
Soit D la distance entre la caméra et le plan de projection :
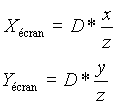
L'œil humain possède un angle d'ouverture de 60° environ. Un choix de D tel que cet angle soit plus grand provoque une distorsion en 'fish-eye'. Une valeur de D trop grande, par contre, donne une vue 'plate' qui manque de relief. On se rapproche alors d'une vue orthogonale sans effet de perspective : c'est comme si la caméra était à l'infini. Usuellement, on prend comme distance D, une valeur de l'ordre de 2,5 fois la principale dimension de l'objet.
Il est souvent utile dans les programmes de CAO de disposer de solides réguliers comme 'briques' pour construire des objets plus complexes. Voici les définitions géométriques de quelques polyèdres réguliers parmi les plus courants. Ils sont donnés sous forme de trois tableaux chaque fois : la tableau des coordonnées des sommets, le tableau des extrémités des arêtes et le tableau des sommets de chaque face.
Il a 4 sommets, 6 arêtes et 4 faces.
Sommet |
X |
Y |
Z |
1 |
1 |
0 |
-Ö 2/4 |
Arête |
Début |
Fin |
|||
1 |
1 |
2 |
|||
Face |
Sommet |
Sommet |
Sommet |
||
1 |
1 |
4 |
3 |
||
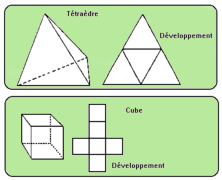
 Il a 8 sommets, 12 arêtes et 6
faces.
Il a 8 sommets, 12 arêtes et 6
faces.
Arête |
Début |
Fin |
|||||||
1 |
1 |
2 |
|||||||
Sommet |
X |
Y |
Z |
||||||
1 |
-1 |
-1 |
-1 |
||||||
Face |
Sommet |
Sommet |
Sommet |
Sommet |
|||||
1 |
7 |
8 |
4 |
3 |
|||||
Les sommets de l'octaèdre sont les centres des 12 faces du cube. Il a donc 6 sommets, 12 arêtes et 8 faces.
Arête |
Début |
Fin |
||||||
1 |
1 |
2 |
||||||
Sommet |
X |
Y |
Z |
|||||
1 |
1 |
0 |
0 |
|||||
Face |
Sommet |
Sommet |
Sommet |
|||||
1 |
1 |
2 |
3 |
|||||
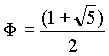
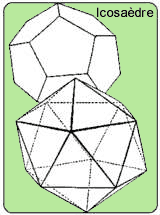
Les 12 sommets de l'icosaèdre sont les sommets de 3 rectangles aux proportions dites 'du nombre d'or' situés dans les trois plans du référentiel OXYZ.
Dans le tableau ci-dessous, on représentera le nombre d'or par le signe f . L'icosaèdre a donc 12 sommets, 30 arêtes et 20 faces triangulaires équilatérales. Les sommets sont des angles pentaèdres.L'icosaèdre et le dodécaèdre sont des solides conjugués : aux faces de l'un correspond un sommet de l'autre et réciproquement.
Sommet |
X |
Y |
Z |
||
1 |
f |
1 |
0 |
||
Arête |
Début |
Fin |
|||
1 |
1 |
9 |
|||
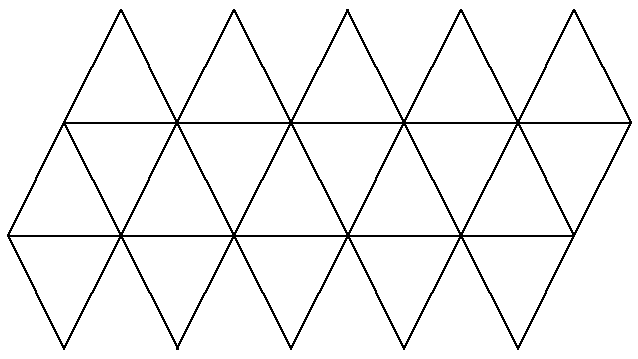
L'icosaèdre développé
 Faces de l'icosaèdre
Faces de l'icosaèdre
Face |
Sommet |
Sommet |
Sommet |
1 |
1 |
9 |
4 |
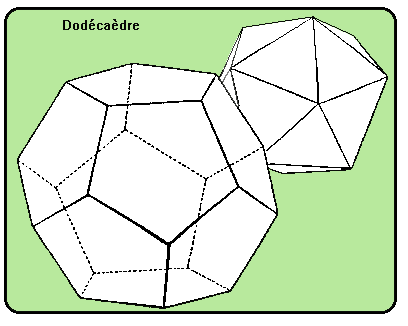
Le dodécaèdre régulier est le quatrième des polyèdres réguliers. Il a 12 Faces, 30 Arêtes et 20 Sommets. Les faces sont des pentagones réguliers convexes. Les sommets sont des angles trièdres.
On peut trouver les sommets du dodécaèdre en prenant le centre des faces de l'icosaèdre.

Arête |
Début |
Fin |
|||||
1 |
1 |
2 |
|||||
Face |
Sommet |
Sommet |
Sommet |
Sommet |
Sommet |
||
1 |
1 |
2 |
3 |
4 |
5 |
||
Les autres polyèdres réguliers sont non convexes. Il s'agit de :
Le petit dodécaèdre étoilé 
Le grand dodécaèdre étoilé 
Le grand dodécaèdre 
Le grand icosaèdre  Définition
Wikipedia des polyèdres
Définition
Wikipedia des polyèdres
Cette page est copyright B.Michel, 2009